강의복습
1. 그래프의 구조를 어떻게 분석할까?
더보기


1) 군집 구조와 군집 탐색 문제
- 군집(Community): 다음 조건들을 만족하는 정점들의 집합
- 집합에 속하는 정점 사이에는 많은 간선이 존재
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재

- 실제 그래프의 군집들은 무엇을 의미할까?
- 온라인 소셜 네트워크의 군집: 사회적 무리(Social Circle), 부정 행위, 조직 내의 분란
- 키워드-광고주 그래프의 군집: 동일한 주제의 키워드
- 뉴런간 연결 그래프의 군집: 뇌의 기능적 구성 단위
- 군집 탐색(Community Detection) 문제: 그래프를 여러 군집으로 잘 나누는 문제
2) 군집 구조의 통계적 유의성과 군집성
- 배치 모형(Configuration Model): 각 정점의 연결성(Degree)을 보존한 상태에서 간선들을 무작위로 재배치하여 얻은 그래프
- 군집성(Modularity)

- 무작위로 연결된 배치 모형과의 비교를 통해 군집성을 측정
- 그래프에서 군집 내부 간선의 수가 월등히 많을수록 성공한 군집 탐색
- 군집성: 항상 -1과 +1 사이의 값 가짐
- 보통 0.3~0.7 정도의 값을 가질 때 통계적으로 유의미하다고 판단
3) 군집 탐색 알고리즘
- 하향식(Top-Down) 알고리즘: Girvan-Newman 알고리즘
- 군집을 연결하는 다리 역할 하는 간선(매개 중심성 높은 간선) 찾아서 순차적으로 제거
- 군집성이 최대가 되는 지점까지 간선 제거
- 매개 중심성(Betweenness Centrality): 해당 간선이 정점 간의 최단 경로에 놓이는 횟수
|
 |
𝝈𝑖,𝑗 : 정점 𝒊로부터 𝒋로의 최단 경로 수 𝝈𝑖,𝑗(𝒙, 𝒚) : 그 중 간선 (𝒙, 𝒚)를 포함한 것 |
- 전체 그래프에서 시작
- 매개 중심성이 높은 순서로 간선을 제거하면서 군집성의 변화를 기록
- 군집성이 가장 커지는 상황 복원
- 이 때, 서로 연결된 정점들, 즉 연결 요소ㄹ르 하나의 군집으로 간주
- 상향식(Bottom-Up) 알고리즘: Louvain 알고리즘
- 개별 정점에서 시작해서 점점 큰 군집 형성
- 군집성 기준으로 합침
- 개별 정점으로 구성된 크기 1의 군집들로부터 시작
- 각 정점을 기존 혹은 새로운 군집으로 이동 (군집성이 최대화되도록)
- 더 이상 군집성이 증가하지 않을 때까지 2를 반복
- 각 군집을 하나의 정점으로 하는 군집 레벨의 그래프를 얻은 뒤 3을 수행
- 한 개의 정점이 남을 때까지 4를 반복
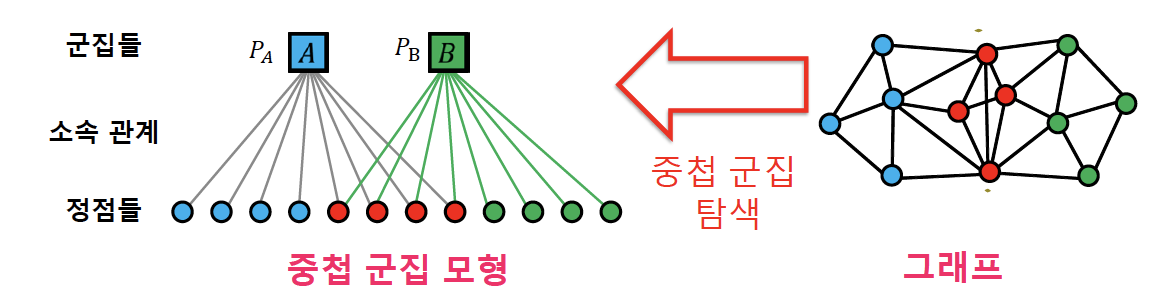
4) 중첩이 있는 군집 탐색
- (완화된) 중첩 군집 모형
- 각 정점은 여러 개의 군집에 속할 수 있음
- 각 군집 A에 대하여, 같은 군집에 속하는 두 정점은 PA 확률로 간선으로 직접 연결
- 두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적
→ 두 정점이 군집 A와 B에 동시에 속할 경우 두 정점이 간선으로 직접 연결될 확률: 1 - (1-PA)(1-PB) - 어느 군집에도 함께 속하지 않는 두 정점은 낮은 확률 𝜖로 직접 연결됨
- 중첩 군집 모형이 주어지면, 주어진 그래프의 확률을 계산할 수 있음
- 각 간선의 두 정점이 모형에 의해 연결될 확률 × 직접 연결되지 않은 각 정점 쌍이 모형에 의해 연결되지 않을 확률
- 그래프가 모형과 얼마나 일치하는지를 의미
- 중첩 군집 탐색: 그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 과정 (=최우도 추정치(Maximum Likelihood Estimate)를 찾는 과정)

- 완화된 중첩 군집 모형: 각 정점이 각 군집에 속해 있는 정도를 실숫값으로 표현 (중간 상태 표현 가능)
5) 실습: Girvan-Newman 알고리즘 구현 및 적용
2. 그래프를 추천시스템에 어떻게 활용할까? (기본)
더보기

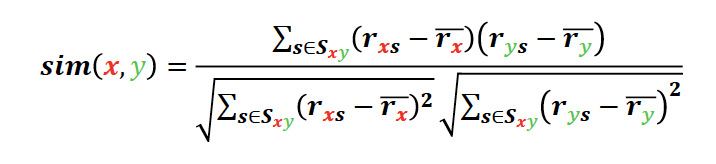

1) 우리 주변의 추천 시스템
- 추천 시스템: 사용자 각각이 구매할만한 혹은 선호할만한 상품 추천
- Amazon.com, 넷플릭스, 유튜브, 페이스북 등
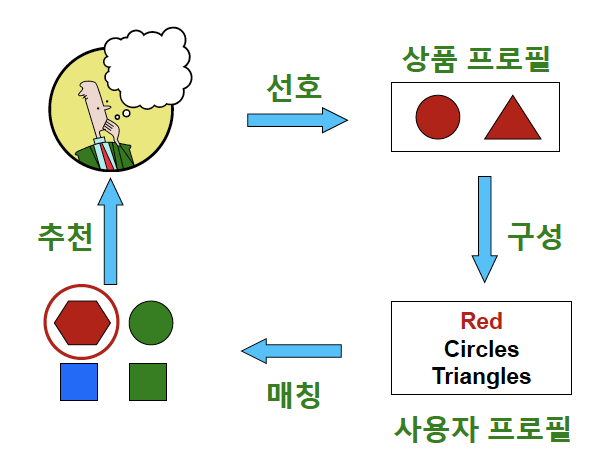
2) 내용 기반(Content-based) 추천 시스템
- 각 사용자가 구매/만족해던 상품과 유사한 것 추천
- 단계
- 상품 프로필(Item Profile) 수집 (해당 상품의 특성을 나열한 벡터)
- 사용자 프로필(User Profile) 구성
- 사용자 프로필과 다른 상품들의 상품 프로필 매칭 (사용자 프로필 벡터와 상품 프로필 벡터의 코사인 유사도 계산)
- 코사인 유사도가 높은 상품 추천

- 장점: 다른 사용자의 구매 기록 필요 없음, 새로운 상품에 대한 추천 가능, 추천 이유 제공 가능
단점: 상품에 대한 부가 정보가 없는 경우나 구매 기록이 없는 사용자는 사용 못 함, 과적합으로 협소한 추천을 할 위험 있음
3) 협업 필터링 추천 시스템
- 단계
- 추천 대상 사용자 x와 유사한 취향의 사용자들을 찾음
- 유사한 취향의 사용자들이 선호한 상품 찾음
- 이 상품들을 x에게 추천

- 취향의 유사성: 상관 계수(Correlation Coefficient)를 통해 측정
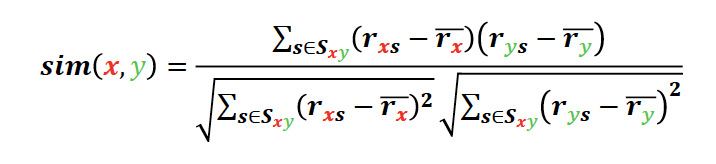
- 취향의 유사도를 가중치로 사용한 평점의 가중 평균을 통해 평점 추정

- 장점: 부가 정보가 없는 경우에도 사용 가능
단점: 충분한 데이터가 누적되어야 효과적, 새로운 상품에 대한 추천이 불가능, 독특한 취향의 사용자에게 추천 어려움
4) 추천 시스템의 평가
- 훈련(Training) 데이터 / 평가(Test) 데이터 분리
- 훈련 데이터를 이용해서 가리워진 평가 데이터의 평점을 추정
- 추정한 평점과 실제 데이터를 비교하여 오차 측정
주로 평균 제곱(근) 오차 사용
|
평균 제곱 오차(Mean Squared Error, MSE) |
평균 제곱근 오차(Root Mean Squared Error, RMSE) |
 |
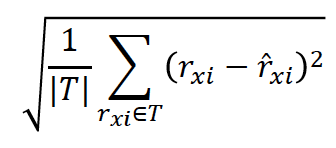 |
5) 실습: 협업 필터링 구현
코멘트
피어세션에서 그래프의 확률에 대한 질문이 나왔다. 나도 강의를 대충 들어서 잘 이해 안 간 채로 넘겼었는데 다시 보니까 그래프가 모형과 얼마나 일치하는지를 의미하는것 같다는 생각이 들었다.
'부스트캠프 AI Tech 1기 [T1209 최보미] > U stage' 카테고리의 다른 글
| Day25 학습정리 - GNN 기초 & GNN 심화 (0) | 2021.02.26 |
|---|---|
| Day24 학습정리 - 정점 표현 & 추천시스템 (심화) (0) | 2021.02.25 |
| Day22 학습정리 - 페이지랭크 & 전파 모델 (0) | 2021.02.23 |
| Day21 학습정리 - 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
| Day20 학습정리 - NLP5 (0) | 2021.02.19 |